

A hindrance factor, h 0, is introduced for odd neutron or odd proton numbers the parameter set of a, b, c, and d is varied in even or odd cases to preserve h 0 = 0.
#HALF LIFE FORMULA FREE#
Its functional form is typically expressed as where a, b, c, d, and h 0 are free adjustable parameters that are varied to reproduce experimental data. The Viola–Seaborg formula is usually used as a simple phenomenological formula.
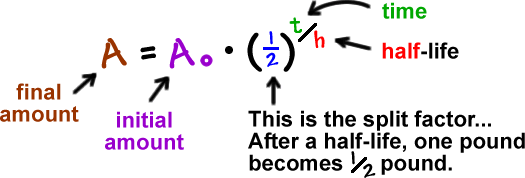
We first derive a phenomenological formula for α-decay half-lives T α from experimental Q α values over a wide nuclidic region. Finally, we give some concluding remarks in section 4. In section 3, we discuss the physical validity of the parameter values and give some results for even–even nuclei and non-even–even nuclei. Furthermore, we discuss applications to superheavy nuclei.Īfter describing the theory of α decay, we construct a phenomenological formula for α-decay half-lives in section 2. We also discuss the effect of the centrifugal potential on nuclear states with a non-zero angular momentum, which is applicable to odd- A and odd–odd nuclei with known spin-parity. We discuss the physical meaning of the functional form and the parameters. In this article, we derive a phenomenological formula for T α based on recent experimentally obtained Q values for α decay. Since those studies focused on the properties of superheavy nuclei of which α decay is just one topic, they provided insufficient theoretical explanation of α decay. In these previous studies, we developed a simple relationship between Q α and T α1/2. Using this formula, we have discussed the decay properties of superheavy nuclei. This mass formula predicts the Q values of various decays including β decay, proton emission, and α decay in the nuclidic region, including the extremely heavy mass region that extends to Z ≈ 175 and N ≈ 320. Our group has developed a nuclear mass formula, which we term the KUTY and KTUY mass formula. One of the main goals in this field is to understand the overall trend for α-decay partial half-lives of nuclei, including nuclei in the superheavy nuclear mass region.

Various nuclear potentials are employed in nuclear physics for a variety of purposes and they give different predictions for shell closures of unknown superheavy nuclei. While this approach may appear promising, it has a considerable problem in that a realistic nuclear potential applicable to the whole nuclear mass region has yet to be determined in nuclear theory. One method for estimating the decay rate or half-life for α decay is to use a realistic (mean-field) nuclear potential that includes deformation to calculate the penetrability of the sum of the nuclear and Coulomb potentials and then estimate the formation probability of an α particle. Of the various decay modes in the heavy and superheavy nuclear mass regions, α decay has the simplest decay mechanism since it involves penetration of the Coulomb and nuclear potentials and formation of an α particle by the nuclear force. This is in contrast to the light and medium-heavy nuclear mass regions in which decay is almost entirely limited to β decay, electron capture, and proton emission. The heavy and superheavy nuclear mass regions have various decay modes, including β decay, α decay, and spontaneous fission. The obtained formula gives half-lives that are two or three times longer than those obtained using the Viola–Seaborg formula in the superheavy nuclear mass region. The root-mean-square deviations from experimental partial half-lives for even–even, odd- A, and odd–odd nuclei are 0.344, 0.740, and 0.940 (in log 10), respectively. The values obtained for the three adjustable parameters are reasonable, in contrast with those of conventional models such as the Viola–Seaborg formula. Parameters in the formula are fixed because they are determined by physical constants except for the following three adjustable parameters: the product of the collision frequency of an α particle and the formation probability, N the distance between the charge radius and the radius of an inner point of the Coulomb barrier, r 0 and the odd-mass hindrance, h 0. It is constructed in a conventional way by considering the penetrability of a charged particle in a spherical Coulomb potential. A phenomenological formula is presented for the partial half-life from the Q value for α decay.


 0 kommentar(er)
0 kommentar(er)
